TEOREMA NORTON

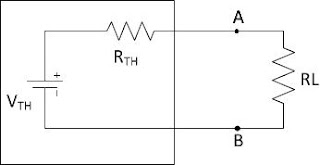
Ingat-ingatlah kembali gagasan-gagasan berikut mengenai teorema Norton. Pada gambar (a) dibawah, arus Norton I_N  didefinisikan sebagai arus beban saat hambatan beban dihubung singkat. Karena ini, arus Norton kadang-kadang disebut dengan arus hubung singkat. Sebagai definisi :

Arus Norton I_N = I_sc

 Hambatan Norton adalah hambatan yang diukur oleh ohmmeter pada terminal beban seluruh sumber diturunkan menjadi nol dan hambatan beban dihubung buka. Sebagai definisi :

Hambatan Norton R_N = R_oc

Karena hambatan Thevenin juga sama dengan R_oc , kita menuliskan :

R_N = R_TH

Penurunan ini menunjukkan bahwa hambatan Norton sama dengan hambatan Thevenin. Apabila anda menghitung hambatan Thevenin sebesar 10 kΩ, segera anda akan mengetahui bahwa hambatan Norton sama dengan 10 kΩ.

Gambar (a) kotak hitam yang mengandung untai linier

IDE DASAR

apa itu teorema norton? jika kita melihat gambar (a). Kotak hitam ini dapat berisi rangkaian apa saja dengan sumber searah dan hambatan linier. Norton membuktikan bahwa rangkaian dalam kotak hitam gambar (a) akan menghasilkan tegangan beban yang sama dengan untai sederhana gambar (b) . Sebagai penurunan, teorema Norton terlihat sebagai berikut :

 

dengan perkataan tegangan beban sama dengan arus Norton dikalikan dengan hambatan Norton yang di paralel dengan hambatan beban.

Sebelumnya kita melihat hambatan Norton setara dengan hambatan Thevenin. Tetapi perhatikan perbedaan lokasi hambatan: Hambatan thevenin senantiasa diseri dengan sumber tegangan, hambatan norton selalu diparalel dengan sumber arus.

Catatan : apabila anda menggunakan aliran elektron, ingatlah hal-hal berikut. Dalam industri, tanda panah dalam sumber arus hampir selalu digambarkan searah dengan arus konvensional. Terkecuali apabila sumber arus digambarkan dengan panah putus-putus. dalam hal ini, sumber mengeluarkan elektron dalam arah yang sama dengan panah putus-putus tersebut.

PENURUNAN TEOREMA

Teorema norton dapat diturunnkan dari prinsip dualitas. Prinsip ini menyatakan bahwa untuk suatu teorema dalam analisis rangkaian elektris ada teorema rangkap (berlawanan) dimana suatu besaran akan menggantikan besaran yang lain. Berikut ini merupakan ringkatan rangkap :

Gambar (c) dan gambar (d) dibawah ini menyimpulkan prinsip dualitas saat diterapkan pada rangkaian Thevenin dan Norton. Ini berarti kita dapat menggunakan salah satu rangkaian itu dalam. Seperti yang akan anda lihat berikut, kedua rangkaian ekuivalen tersebut cukup bermanfaat. Kadang-kadang, lebih mudah untuk menggunakan rangkaian Thevenin. Pada saat lain, kita menggunakan Norton. Semua tergantung pada soal-soal yang khusus. Tabel (a) merupakan ringkasan langkah-langkah untuk mendapatkan besaran-besaran Thevenin dan Norton.

Gambar (c) mengubah Thevenin menjadi Norton

 

 

Gambar (d) Mengubah Norton menjadi Thevenin

 

HUBUNGAN ANTARA RANGKAIAN THEVENIN DAN NORTON

Kita telah mengetahui bahwa hambatan Thevenin dan Norton memiliki nilai yang sama, tetapi di lokasi yang berbeda. Hambatan thevenin diseri dengan tegangan sumber dan hambatan Norton diparalel dengan sumber arus.

Kita dapat lagi menurunkan dua hubungan sebagai berikut. Kita dapat mengubah setiap rangkaian Thevenin menjadi rangkaian Norton, seperti yang terlihat dalam gambar (c) di atas tadi. Pembuktian secara langsung. Hubung singkatkan terminal AB pada rangkaian Thevenin dan anda akan mendapatkan arus Norton.

Tabel (a) Besaran Thevenin dan Norton

 

 

Penurunan ini mengatakan bahwa arus Norton sama dengan tegangan Thevenin dibagi dengan hambatan Thevenin.

Dengan cara yang sama, kita dapat mengubah setiap mengubah setiap rangkaian Norton menjadi Thevenin seperti yang terlihat pada gambar (d). Tegangan rangkaian terbuka adalah

Penurunan ini mengatakan bahawn tegangan thevenin  sama dengan arus Norton dikalikan dengan hambatan Norton.
gambar (c) dan (d) menyimpulkan Persamaan untuk mengubah salah satu rangkaian menjadi rangkaian yang lain.

Read More

TEOREMA THEVENIN

DEFINISI TEGANGAN DAN HAMBATAN THEVENIN

Sebuah teorema merupakan pernyataan yang dapat kita buktikan secara matematis. Karena inilah, teorema bukan merupakan suatu definisi atau hukum. Sehingga, kita mengklasifikasikan teorema sebagai suatu penurunan.  Pada gambar (a)  di bawah ini tegangan Thevenin V_TH didefinisikan sebagai tegangan yang melewati terminal beban saat hambatan beban terbuka. Karena ini, tegangan thevenin kadang-kadang disebut dengan tegangan untai terbuka. Definisinya :

Tegangan Thevenin : V_TH = V_OC

Hambatan Thevenin didefinisikan sebagai hambatan yang diukur antar-terminal pada gambar (a) saat seluruh sumber dibuat nol dan hambatan beban dibuat. Sebagai definisi :

Hambatan Thevenin : R_TH = R_OC

Gambar (a) kotak hitam yang memiliki untai linier di dalamnya

 

 

 

Ada dua hal penting dalam mencari hambatan Thevenin. Menurunkan sumber menjadi nol memiliki arti yang berbeda antara sumber tegangan dan sumber arus. Ketika anda menurunkan sumber tegangan menjadi nol, secara efektif Anda menghubung singkat sumber karena hal tersebut merupakan satu-satunya cara untuk menjamin tegangan nol ketika arus mengalir melalui sumber tegangan. Ketika anda menurunkan sumber arus menjadi nol, secara efektif anda menghubung buka sumber karena hal tersebut merupakan satu-satunya cara untuk menjadi arus nol ketika ada tegangan pada sumber arus. Secara ringkas :

Untuk membuat sumber tegangan menjadi nol, hubungkan singkat sumber Untuk membuat sumber arus menjadi nol, hubungkan buka sumber

Gambar (b) Rangkaian Thevenin

PENURUNAN TEOREMA

Jika kita melihat gambar (a), kotak hitam ini mengandung rangkaian dengan sumber searah dan hambatan linier (hambatan linier tidak berubah dengan naiknya tegangan). Thevenin dapat membuktikan bahwa betapapun rumitnya suatu rangkaian dalam kotak hitam pada gambar (a), rangkaian tersebut akan menghasilkan arul beban yang sama dengan rangkaian sederhana  pada gambar (a). Penurunannya :

 

Teorema Thevenin merupakan alat bantu pembangkit tenaga listrik insinyut dan teknisi menggunakan teorema ini terus menerus. Elektronika mungkin tidak akan seperti sekarang ini tanpa teorema thevenin. Teorema ini tidak hanya menyederhanakan perhitungan, tetapi juga memungkinkan kita untuk menjelaskan operasi rangkaian yang tidak mungkin dijelaskan dengan menggunakan persamaan Kirchoff.

Read More

Menggunakan Projectboard

untuk bagian atas dan bawah pada nomor 1 dan 2 masing-masing terhubung secara horizontal, artinya lobang yang dilingkari semua itu semua terhubung. artinya jika ingin menambahkan lagi kesamping, tinggal diberi jumper.

untuk bagian 3 dan 4 masing-masing terhubung secara vertikal, sampai dengan yang dilingkari.

spasi ditengah digunakan untuk komponen seperti IC atau microkontroller.

sedangkan bagian dibawah sama penggunaannya seperti nomor 1 dan 2

Read More